深入探討 F# 之 Function

強悍的 FP 支援令人著迷

F# 身為 function first-first language，最迷人的當然就是 function 部分。

Version

.NET Core SDK 2.4.1
F# 4.1

Syntax

1
let f x = x + 1
  • 由於 function 也被視為 value，因此同樣使用 let 定義 function
  • f 為 function name，x 為 parameter，之間以 space 隔開
  • = 右側為 function 定義
  • 由於 pure function 要求要有回傳值，所以 x + 1 將被回傳，不用加上 return
  • 不必使用 ; 結束

Scope

1
2
3
4
5
6
let list1 = [ 1; 2; 3]
let list1 = [] // module : error, function : []
let function1 =
   let list1 = [1; 2; 3]
   let list1 = []
   list1 // []
  • 當 value 名稱相同時，若在 module 會 compile error，若在 function 內則是 後蓋前，因此 list1 皆為 []
1
2
3
4
5
let list1 = [ 1; 2; 3]
let sumPlus x =
// OK: inner list1 hides the outer list1.
   let list1 = [1; 5; 10]
   x + List.sum list1
  • 若 function 內的 value 與 function 外的 value 名稱相同，則 function 內的 value 會蓋掉 (shadow) function 外的變數，因此 sumPlus 的 list 為 [1; 5; 10]

雖然 value 相同，F# 會啟動 shadow 機制，但實務上還是不建議重複使用 value 名稱，將造成維護上的困難

Parameter

1
let f (x : int) = x + 1
  • 亦可在 parameter 加上型別，必須使用 ()，在 parameter 名稱之後加上 : 與 型別
1
let f x = x + 1
  • 儘管 paramter 不加上型別，因為 F# 的 Type Inference 機制，compiler 會自動由 function body 推導出 parameter 型別

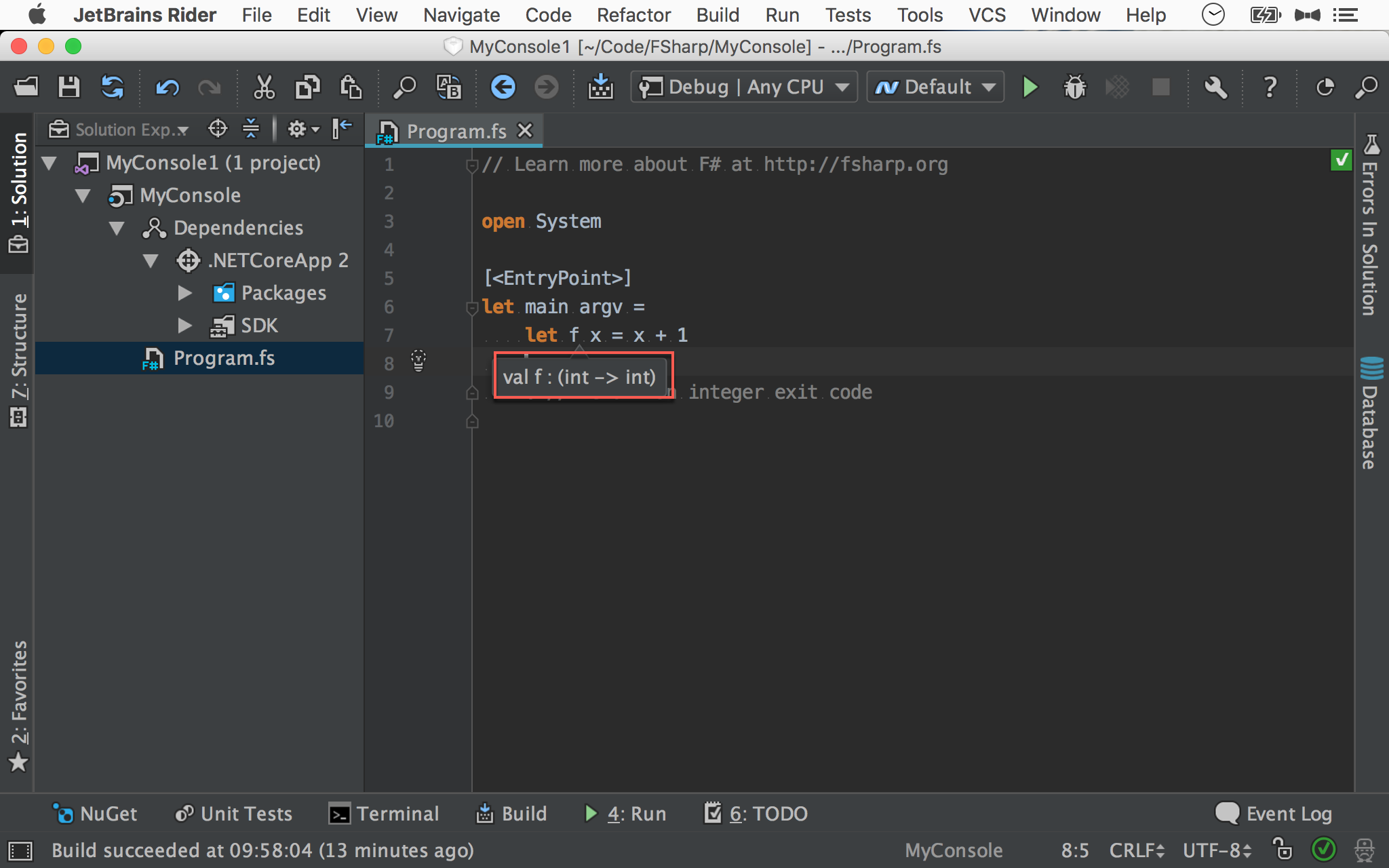
function000

只要將滑鼠移動到 parameter，就可看到其型別為 int。

F# 的 parameter 雖然不用寫型別，但不代表 F# 沒有型別，而是因為其強悍的 Type Inference 機制，讓我們可以少打點字，閱讀上真的想知道型別，就靠 IDE 顯示型別

實務上建議 parameter 不用寫型別，使用 Type Inference 即可

1
let f x = (x, x)

若 Type Inference 無法推導出型別，就視為 泛型。

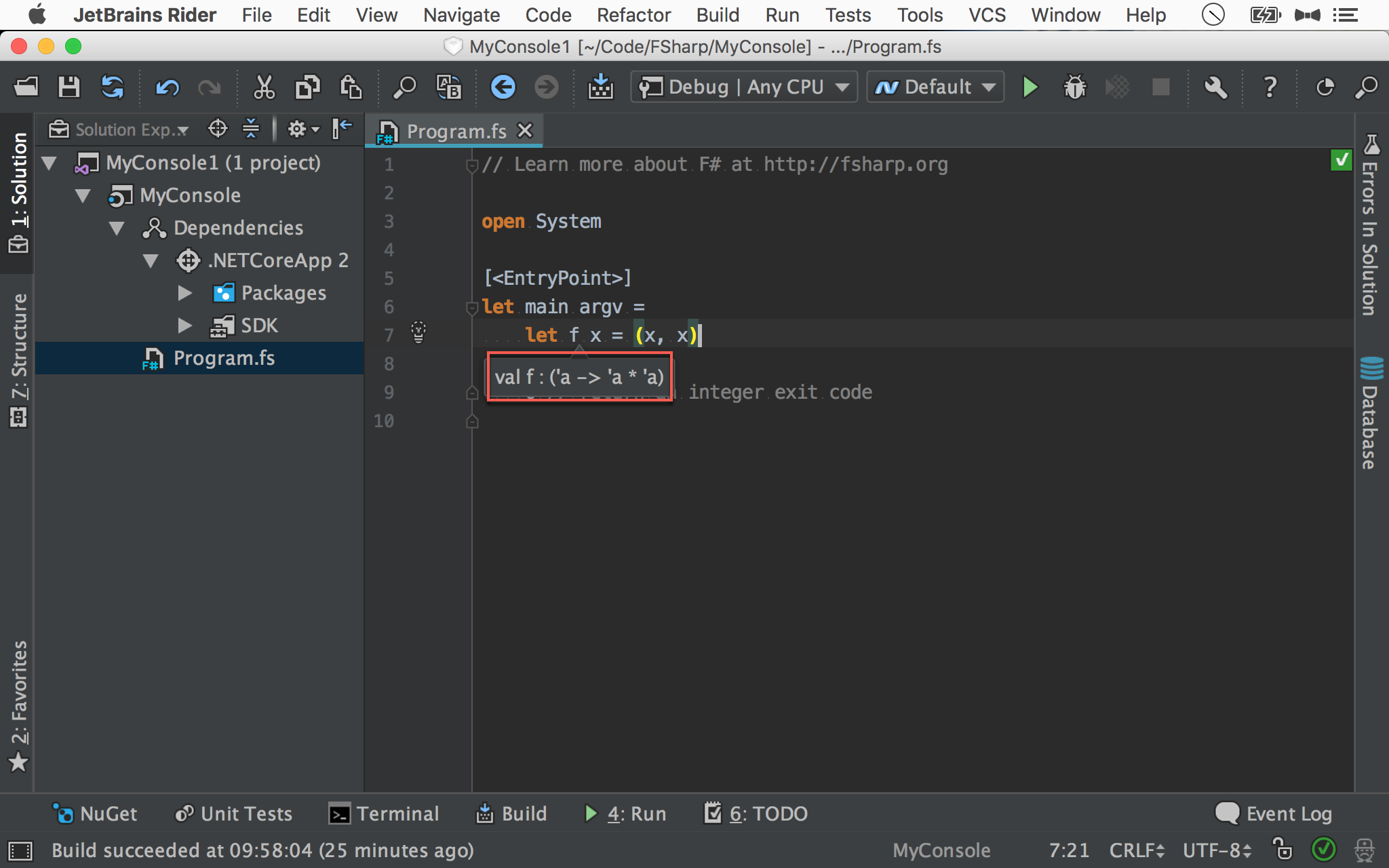
function001

由於 Type Inference 無法由 function body 推導出型別，所以啟動 Automatic Generalization 機制，其中 'a 為自動推導出的 泛型。

在 F# 要使用 泛型，只要不寫型別，且無法推導出具體型別，就被視為 泛型，syntax 比 C# 精簡很多

Function Body

1
2
3
4
let cylinderVolume radius length =
    // Define a local value pi.
    let pi = 3.14159
    length * pi * radius * radius

  • 若 function 內的程式碼不只一行時，則 = 換行之後並加以縮排，不必使用 {}

  • Function 內的 value 的 scope 僅限於 function 內，因此 pi 只有 cylinderVolume 可讀取

C# 程式碼中，{} 佔了不少行數，F# 利用縮排取代 {}，程式碼顯的更清爽，且輸入 tab 速度也比 {} 還快

Return Value

1
2
3
4
let cylinderVolume radius length =
    // Define a local value pi.
    let pi = 3.14159
    length * pi * radius * radius
  • Function 最後一行的 expression 或 value 都視為 return 值，因此回傳值為 length * pi * radius * radius expression
  • Function 最後一行的 expression 或 value 的型別會被推導為 return type，因為 pi 為 float，所以 return type 被推導為 float

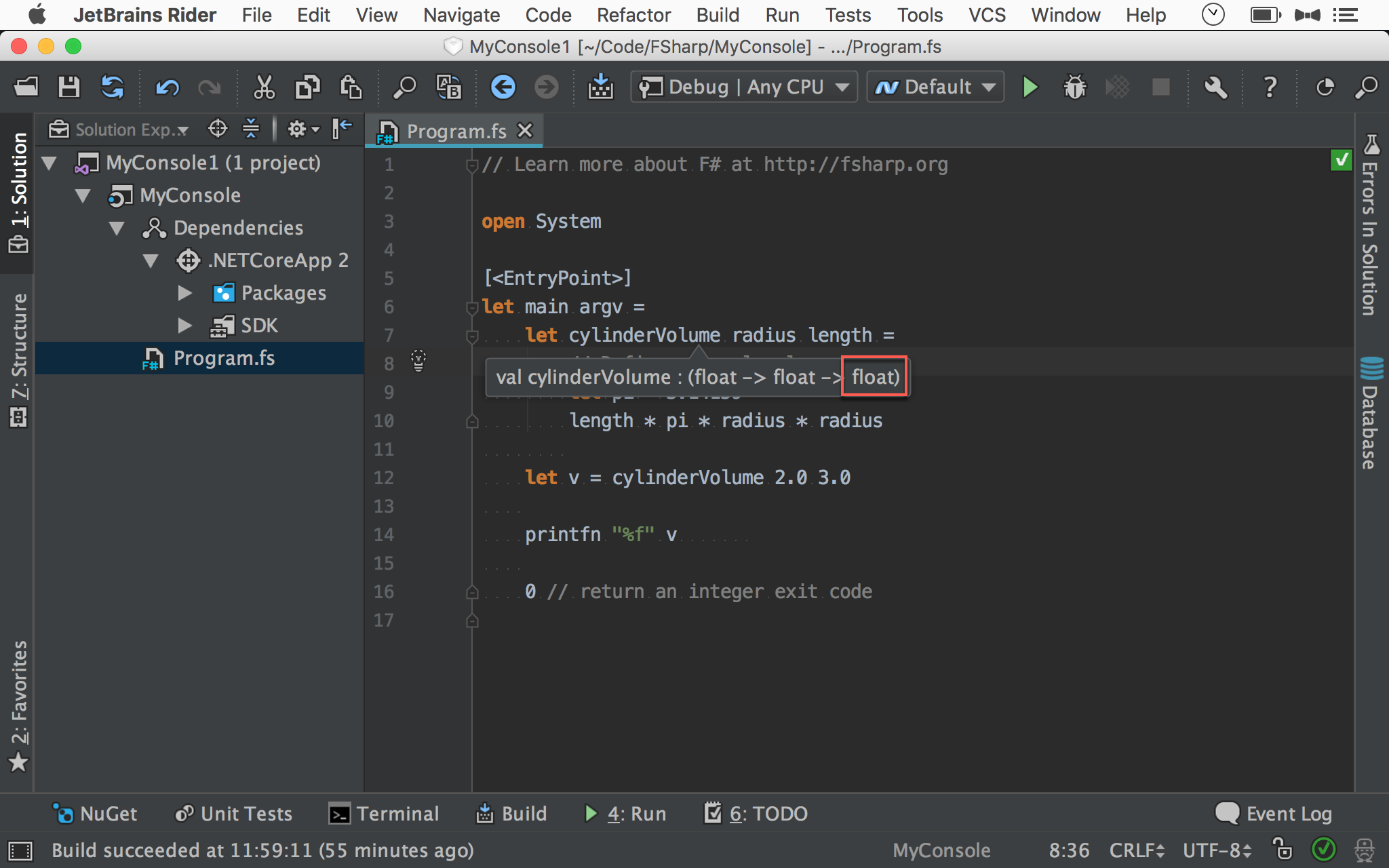
function002

只要將滑鼠移動到 function，就可看到其 return type 為 float。

C# 程式碼中會到處充滿 return，F# 很聰明的用最後一行的 value 或 expression 當回傳值，讓程式碼更精簡

1
2
3
4
let cylinderVolume radius length : float =
   // Define a local value pi.
   let pi = 3.14159
   length * pi * radius * radius
  • 亦可為 return type 加上型別，只要在最後加上 : 與 型別
1
2
3
4
let cylinderVolume (radius : float) (length : float) : float =
   // Define a local value pi.
   let pi = 3.14159
   length * pi * radius * radius
  • 亦可為 parameter 與 return type 全部加上型別

實務上建議不用替 parameter 與 return type 加上型別，使用 Type Inference 即可

Calling a Function

1
let vol = cylinderVolume 2.0 3.0
  • Argument 不需使用 ()，只要與 function name 用 space 隔開即可
  • Argument 之間不需要 ,，只需用 space 隔開即可

傳入 parameter 不需 () 與 ,，減少打字時間

Currying

1
2
3
4
5
let smallPipeRadius = 2.0
let bigPipeRadius = 3.0

let smallPipeVolume = cylinderVolume smallPipeRadius
let bigPipeVolume = cylinderVolume bigPipeRadius
  • 若對 function 只傳入部分 parameter，將回傳一個新的 function，可將剩下的 parameter 繼續傳給新的 function，因此可先將 radius 傳入 cylinderVolume，產生smallPipeVolume 與 bigPipeVolume 兩個新的 function
1
2
3
4
5
6
let length1 = 30.0
let length2 = 40.0
let smallPipeVol1 = smallPipeVolume length1
let smallPipeVol2 = smallPipeVolume length2
let bigPipeVol1 = bigPipeVolume length1
let bigPipeVol2 = bigPipeVolume length2
  • 再傳入 cylinerVolume 剩餘的參數 length 給 smallPipeVolume 與 bigPipeVolume，即可得到與 cylinderVolume 相同的結果

Q : 為什麼要使用 Currying ?

傳統 function 必須在所有 argument 都準備好後，才可以呼叫 function，且 function 是立即執行。

若使用 currying，可分階段將 argument 傳入 function，並回傳新的 function，直到所有 argument 都具備後，function 才會真正執行。

Q : 實務上何時會使用 Currying ?

  1. Argument 無法一次提供，需要逐次提供時
  2. Function 的某些重要 argument 先由底層 library 提供，並傳回新的 function 給 client，client 只要提供剩下的參數即可
  3. 實現 Decorator Pattern

Recursive Function

1
let rec fib n = if n < 2 then 1 else fib (n - 1) + fib (n - 2)
  • 若在 function body 需要呼叫 function 本身，在 function name 前面加上 rec，表示此為 recursive function

有些演算法的數學，就是使用 recursive 表示，若要改用 loop 改寫反而有難度，若直接用 recursive 表示，不僅能忠實呈現演算法，也比較容易 implement

Function Value

1
let apply1 (transform : int -> int ) y = transform y
  • FP 的核心概念就是將 function 當成 value 看，稱為 Function Value。
  • 除了與 value 一樣使用 let 定義 function 外，也跟 value 一樣，可以將 function 當成 function 的 parameter，因此 apply 為 function， transform 為 apply1 的 parameter，但 transform 為 function，其 type 為 int -> int，此為 transfom 的 input 為 int，output 為 int
  • F# 以 -> 定義 function 的 signature type
1
2
let increment x = x + 1
let result1 = apply1 increment 100
  • 因此可定義 increment function，再將 increment 傳入 apply
1
2
3
let apply2 (f: int -> int -> int) x y = f x y
let mul x y = x * y
let result2 = apply2 mul 10 20
  • 當 function 有多個 parameter 時，其型別表示為多個 -> 串起來，如 let mul x y = x * y，則 mul 的型別為 int -> int -> int

Q : 為什麼多 paramter 要以 -> … -> 表示

別忘了 F# 的 Currying，如 mul 相當於以下寫法

1
2
let mul2 = mul 2
let mul2x3 = mul2 3

所以多個 parameter 就相當於 1 個 parameter 的 function 連續呼叫多次，因此相當於 -> 串起來多次。

Lambda Expression

1
2
let result3 = apply1 (fun x -> x + 1) 100
let result4 = apply2 (fun x y -> x * y ) 10 20
  • Function 的 parameter 可以傳入 function，除了使用 let 先定義好 function 外，也可以直接在 arguemtn 以 unnamed function 或 anonymous function 表示，這就是 Lambda Expression
  • Lambda Expression 以 fun 開頭，使用 -> 取代 =
1
2
let increment = fun x -> x + 1 // let increment x = x + 1 is better
let result1 = apply1 increment 100
  • 就語法而言，的確可以 let 配合 fun ，但實務不建議這種寫法，因為 increment 的 parameter 必須由 fun 才能看出，較不直覺
  • 建議 let 與 fun 不要混用，將 fun 用在直接傳入 function 的 argument 即可

Function Composition

1
2
3
4
let function1 x = x + 1
let function2 x = x * 2
let h = function1 >> function2
let result5 = h 100
  • 若有兩個 function，需求是先執行 function1 ，並將 function1 的結果傳入 function2，可使用 >> 將兩個 function 組合成新的 function

在數學，我們常常有 fog(x) = f(g(x))，若以 F#，可使用 let fog = g >> f 表示，重點還是 從左到右，可讀性更數學更高

Pipelining

1
let result = 100 |> function1 |> function2
  • 將 100 傳入 function1，並將結果傳入 function2

在 imperative language，我們會寫成 function2(function1(100))，只要層數夠多，程式碼可讀性就不高，而且還必須 從右到左，但使用 pipelining 之後，無論幾層都很容易閱讀，並且還是 從左到右。

Conclusion

  • 本文介紹了 F# 所有的 function 功能，一些看似直覺的如 Currying、Function Composition 與 Pipelineing ….，在 F# 寫法都很直覺，但在大部分非 FP 語言實現都有難度，這就是 F# 可愛的地方

Reference

Microsoft Docs, Functions

2018-03-12
▲